- Flex PCB Blog
- PCB Assembly Blog
- FPC Research Blog
- Preparation of FPC based on ultrasonic spraying method_4_Experimental Results
- Preparation of FPC based on ultrasonic spraying method_3_Experimental Procedure
- Preparation of FPC based on ultrasonic spraying method_2_Experimental Platform and Principle
- Preparation of FPC based on ultrasonic spraying method_1_abstract
- Research on Layout Design Method of Ultra-thin FPC_4_Analysis of Layout Design Methods
- Research on Layout Design Method of Ultra-thin FPC_3_Analysis of Layout Design Methods
- Research on Layout Design Method of Ultra-thin FPC_2_Analysis of Layout Design Methods
- Research on Layout Design Method of Ultra-thin FPC_1_introduction
- Research progress on polyimide FPC_2_the field of FPC
- Research progress on polyimide FPC_1_Introduction
- Analysis of Vibration Characteristics of FPCBs _4_Summary
- Analysis of Vibration Characteristics of FPCBs _3_Finite Element Analysis
- Analysis of Vibration Characteristics of FPCBs _2_Theory of Vibration Analysis
- Analysis of Vibration Characteristics of FPCBs Under Random Vibration_1_Introduction
- Design Methods for FPCBs_5_Practical Application
- Design Methods for FPCBs_4_Electrical Circuit Design and Examples
- Design Methods for FPCBs_3_Structure Design Method and Examples
- Design Methods for FPCBs_2_Component Selection Methodology and Examples.
- Research on Design Methods for FPCBs
- Application of MPW technique for FPCBs _4_Summary
- Application of MPW technique for FPCBs_3_Experimental results
- Application of MPW technique for FPCBs_2_Experimental setup
- Application of MPW technique for FPCBs_1_Principle of MPW
- Application of FPCB in PC motherboards_4_ Results and discussion
- Application of FPCB in PC motherboards_3_ Numerical analysis
- Application of FPCB in PC_2_ Experimentation
- Application of FPCB in PC motherboards
- A Bus Planning Algorithm for FPC Design _4_Experimental result
- A Bus Planning Algorithm for FPC Design _3_Proposed Algorithm
- A Bus Planning Algorithm for FPC Design _2_Preliminaries
- A Bus Planning Algorithm for FPC Design _1_Introduction
Analysis of Vibration Characteristics of FPCBs _2_Theory of Vibration Analysis
2.Theory of Vibration Analysis
Modal shapes are inherent dynamic characteristics of a structure, which can describe the specific vibration conditions of the structure in a particular frequency domain, directly affecting the dynamic performance of the structure. When a structure is excited by spontaneous excitation or external excitations such as impacts, the resulting vibration is composed of modal shapes at various natural frequencies superimposed with different coefficients. When the excitation frequency is close to or equal to one of the structure's natural frequencies, the entire structure will exhibit the specific vibration form corresponding to that mode, and the vibration level under this condition will be significantly enhanced.
The generalized vibration differential equation of a structure under external excitation can be expressed as:
![]()
In the equation, M, C, and K represent the mass matrix, damping matrix, and stiffness matrix of the structure, respectively, and they are all positive definite symmetric matrices. U is the displacement response of the structure, and P(t) is the excitation load.
If the structure is undamped or the damping is in the form of proportional damping or other classical damping, the resulting modal vectors are all real vectors. The vibration differential equation can be written as:
![]()
The modal vector matrix Φ and the natural frequency matrix p of the structure are orthogonal, meaning that:
![]()
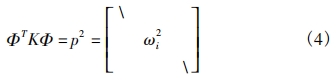
When there is classical damping, the following relationships hold:
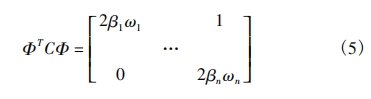
The displacement vector U of the structure and the modal response vector Y are related by a transformation:
![]()
Substituting equation (6) into equation (1), we obtain the vibration differential equation expressed in terms of the modal response vector:
![]()
Multiplying equation (7) on the left by Φ^T and using equations (3) to (5), we get:
![]()
Where PΦ and CΦ are defined as:

Extracting any single equation from equation (8), we get:
![]()
The equation is known as the dynamic equation in modal coordinates, and it can be solved using the same methods as for single-degree-of-freedom systems. From this, we can obtain the impulse response function for equation (11):
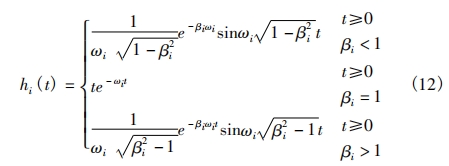
Combining equations (12), we obtain the modal impulse response function matrix:

The frequency domain response function corresponding to h_i(t) is given by:
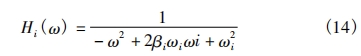
Combining equations (14), we obtain the modal frequency domain response function matrix:
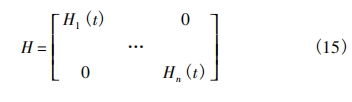
The components of the modal response vector are obtained as follows:




