FPCWAY

A Bus Planning Algorithm for

FPC Design in Complex Scenarios_3_Proposed Algorithm

In this section, we introduce the specific  optimiza- tion  algorithm  of  the  CP  location  problem.  First,  we give an overview of the whole process and then  intro- duce the proposed algorithm in detail.

Fig.4 is the overall flow of the proposed algorithm, which  can  be  divided  into  two  parts:   (1)  Build  the whole  board  bus  topologically  non-crossing  sequence; (2) CP iterative optimization.

1. Bus topologically non-crossing sequence

Traditional  DPS  requires  routing  iteration  to  get the best sequence expansion. This paper only uses the idea  of erasing the  same  symbol  of the  sequence  after expansion  to  judge  that  the  topology  does  not  cross; that  is,  after  expanding  into  a  circular  sequence,  as shown in Fig.5(a), the bus B and A expand into a circu- lar sequence  BAAB, we  can observe that symbol  A  is repeated due to the concatenation, it means that net A can be  connected  without  crossing.  If a  sequence  can- not  be  completely  erased,  as  shown  in  Fig.5(b),  it  is proved that the bus still in the sequence cannot be on the same layer.

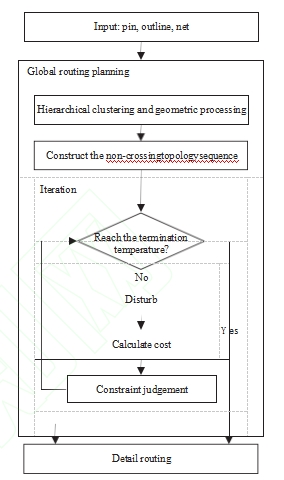
Fig.4. The flow of the proposed algorithm

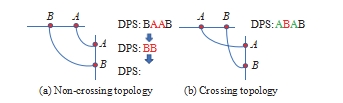
Fig.5.using DPS to judge whether there is a crossing.

The  channel  area  of  FPC  cannot  be  detoured  or punched when routing due to the direct guidance of the outline and the limitation of materials, so the topologic- al  non-crossing  must  correspond  to  the  non-crossing paths of the actual routing. Besides, based on the PAI model, we  can  first  deal  with  the  connection  between buses  and  then  handle  the  single  net  in  the  bus. Fig.6(a) shows the topological connection based on PAI; it can be seen that the connection relationship of FPC buses has many topological crossings. In this step, the specific location of the CPA in the DPS sequence  can- not  be  determined  due  to  the  net  can  detour  in  the CPA. Therefore, the processing of the CPA is turned to the disturbance, and we only considered the non-cross- ing topological of SPA in this step. Fig.6(b) shows the connection  relationship  after  shielding  the  CPA,  and the  sequence  expanded  in  clock  sequence  is  shown  in Fig.7(a). This sequence is finally mapped to the bound- ary line of each SPA as shown in Fig.7(b). This order will not be changed after it is determined, which means that as  long  as the  boundary  satisfies this  order  rela- tionship,  there  will  be  no  topological  cross  between buses, and it will be used as a constraint for the  sub- sequent iteration process. The single net in  CPA  con- nected with SPA is randomly inserted between bus  se- quences during the subsequent disturbance.

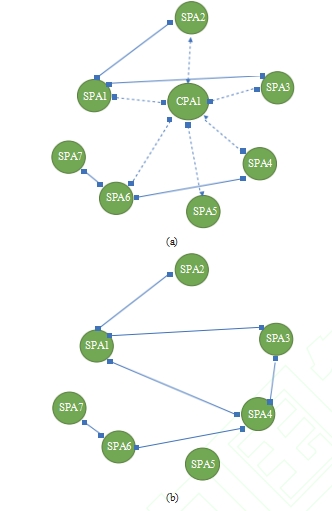
Fig.6

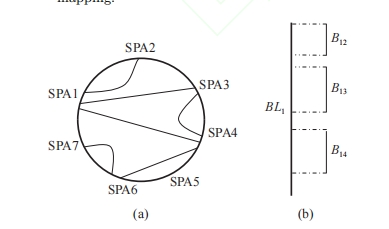
Fig.7

2.  CP iterative optimization

In this section, we introduce the cost system and disturbance strategy of iteration in detail. We use simulated annealing (SA) to comprehensively  consider the costs and constraints of SPA and channel. SPA and channel have different characteristics, so the two regions need to be considered separately to achieve better results.

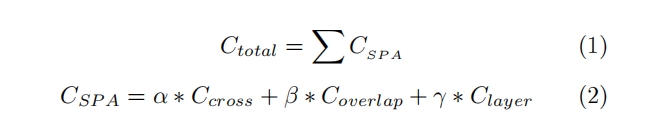
where is the cost of SPA, is the cross cost of the SPA, is the overlapping cost of the fly- line and obstacle in SPA, is the exchange layer cost. The goal is to minimize the total cost  . ,     are custom parameters and the values used in the experiment are 100、1、10, respectively. This is be- cause the unit is length, and thus we convert other units into length units. The selected key parameters of SA are listed in Table 1.

T-max is the start temperature, T-min is the  ter- mination temperature, Iter is the Markov chain length.

1)  Fly-line crossing cost

The fly-line crossing has certain representative sig- nificance  in  the  SPA,  if  the  fly-line  crosses,  it  means that a detour is necessary to solve the problem.  Mul- tiple fly-line crosses at the same time may lead to the inability to connect the net no matter how it is detour. As such, the cross cost is considered, which can be given as：

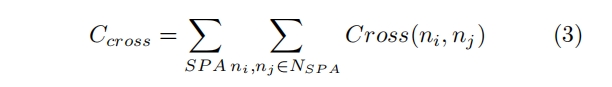
where  Cross(ni , nj )  represents  the  crossing  of  net  ni and nj   in SPA. NSPA  is the total net in SPA.

2)  Overlapping cost

Considering both the SPA and the CPA, there always exist various  obstacles, such as components and forbidden routing areas, and the netlist  must  bypass these obstacles, which bring additional length. It is realistic to measure the manual routing, which can be expressed as

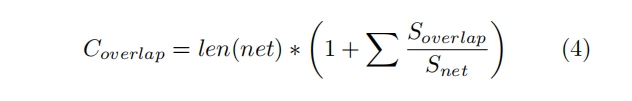
where len(net) is the length of the fly-line, Soverlap   is the area where the obstacle overlaps the rectangle with this fly-line as the diagonal, Snet  is the area of this rect- angle, which is shown in Fig.8.

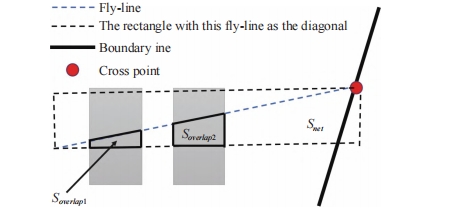
Fig.8

3)  Exchange layer cost

It is often difficult for topology strategy to  estimate the  real  punching  information;  however,  considering a single net, its optimal punching quantity can be determined.  Especially,  if the  starting  pin  and  ending pin of a net are located on the same layer, it is better not to change the layer; otherwise, it is encouraged to use only one via if the type of via allows. In this way, one can simplify counting the number of vias:

where Via(ni ) indicates the cumulative number of holes punched in the net ni , this value can be obtained by counting the number of changes in the layer of the CP to which the net ni  belongs in the PAI model.

4) Non-crossing constraint in the channel

Bus non-crossing constraint only ensures that thereis no cross between different SPAs; otherwise it would cause serious cross overs when the net from CPA is inserted into the bus sequence randomly. We know the layer assignment of CP after disturbance, so it is promising to judge the topology cross of each layer of each channel. For example, as shown in Fig.9,  BL1is the boundary line of SPA1 , B12 , B13 and B14 are the relative  order of bus mapping on the boundary line after non-crossing topology expanded. A single net from CPA is randomly inserted into the interval  between buses during the disturbance, then perform sequence cross judgment again. If there is the cross in the channel the random results will be passed.

3.  Random disturbance strategy

Both the fly-line crossing cost and obstacle overlapping cost are dependent on the location of CPs, and it is often inconvenient to directly disturb the coordinate of the CPs. As such, we choose to change the location of the point indirectly by disturbing the width of the net to achieve the purpose of disturbing the location of the CPs. The minimum distance constraint  between nets shall be strictly guaranteed. The net connect to the CPA will be randomly inserted into the bus interval on the corresponding boundary at each iteration; this is be- cause in the previous step B only the net from the SPA is considered, and the net from the CPA cannot join the circular  sequence formed by the SPA. The net in the bus will also change layers or change the order in sequence randomly.